Александр Алахвердянц знакомит с новинками в двухмерных и трехмерных решателях — продуктах, которые разрабатываются в группе C3D Solver.
Что такое решатели? Решатели — это библиотеки, которые позволяют накладывать связи на геометрические объекты. Эти связи мы называем ограничениями. Они бывают двух видов: логические (касания, симметрии, совпадения) и размерные (угловой и линейный размеры, паттерны). Кроме того, мы предоставляем функционал анализа степеней свободы, минималистичного драггинга и логирования вызовов API. Логирование вызовов API значительно помогает при составлении баг-репортов.
Первая и главная новинка группы C3D Solver в этом году — это появление нового типа объектов, а именно двумерных паттернов.
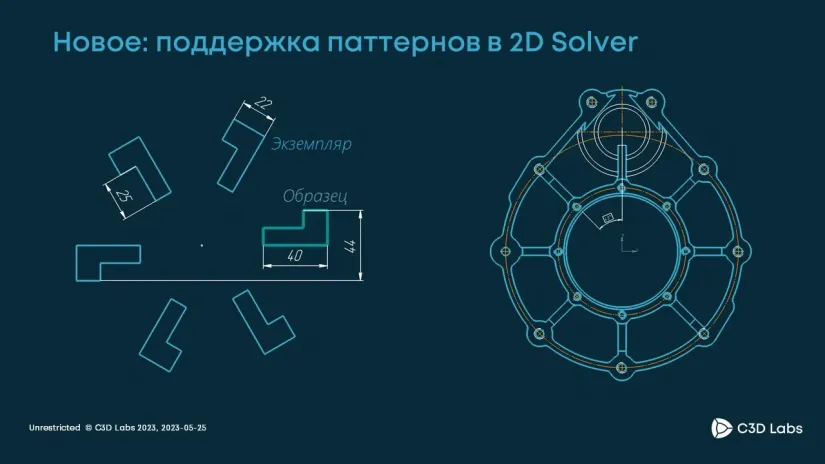
Под двумерными паттернами мы понимаем множество объектов, которые рождены как копии от некоторого образца и расположены на плоскости относительно этого образца согласно заданному закону. Этот закон может быть как простым, например в случае с линейным сдвигом, так и очень сложным.
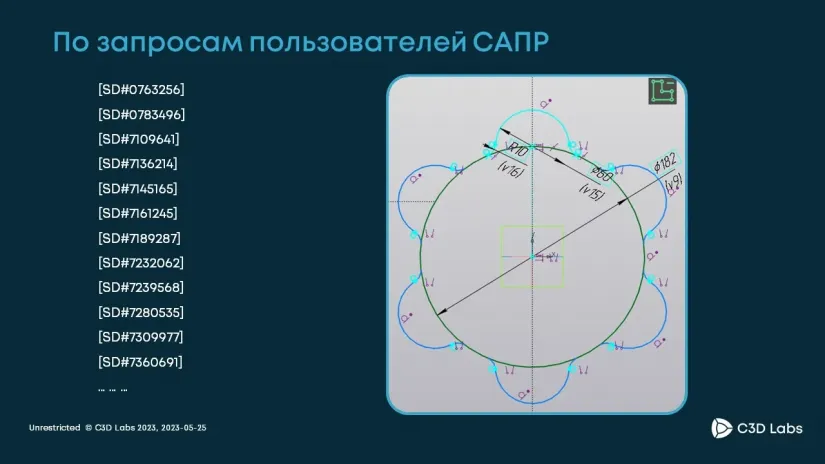
Для начала мы проанализировали широкий набор запросов от наших пользователей. В чем была проблема?
Так как ранее мы не предоставляли такой функционал, то разработчикам САПР и непосредственно инженерам приходилось самостоятельно создавать копии большого числа одинаковых объектов при моделировании эскизов, самостоятельно накладывать на них ограничения, поддерживать связи. Это было крайне сложно. Более того, когда объектов становилось слишком много, выполнять эти задачи было практически невозможно.
Поэтому мы реализовали в нашей библиотеке паттерны.
Когда мы их реализовывали, то заботились об интересах двух сторон. Первая — это инженеры. Важно было предусмотреть, чтобы им было легко работать с массивами компонент. Вторая — это сторона разработчиков, как САПР, так и математического ядра.
Что важно для инженеров?
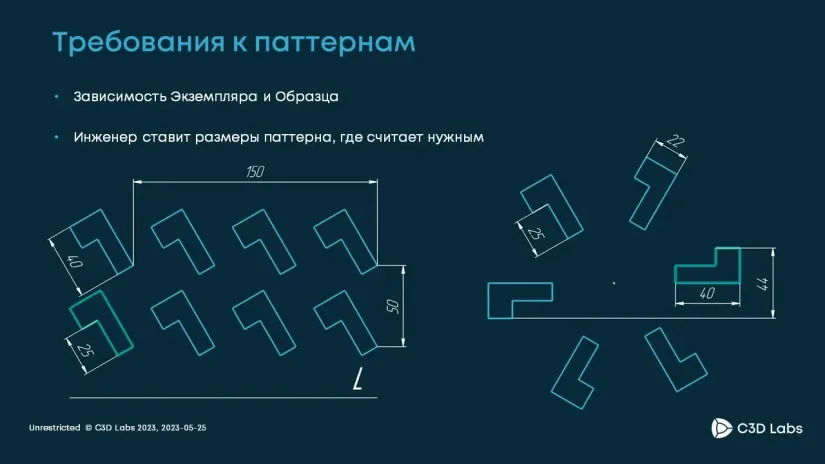
Как уже было обозначено, в паттернах есть некоторая неявная односторонняя связь между образцом и копиями. Когда инженер моделирует что-то в эскизе, ему не требуется информация об этой связи. Ему необходимо, чтобы все объекты были равноправными, а на копии можно было бы накладывать точно такие же ограничения, как на образец. Мы достигли этой цели. Помимо этого, когда инженер моделирует паттерны, ему нужна возможность в произвольном порядке добавлять копии, удалять их, редактировать. Эту возможность мы тоже реализовали.
Что важно для разработчиков САПР?
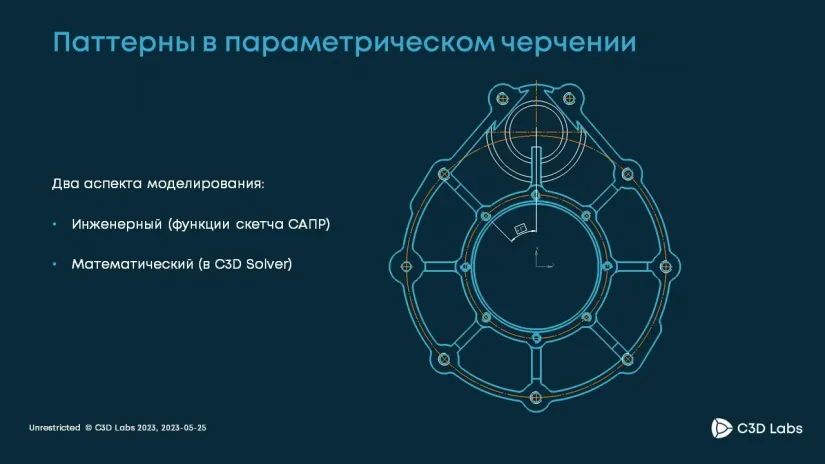
С учетом многообразия паттернов и стремления удовлетворить все потребности пользователей конечного приложения разработчикам САПР важно предоставлять условия для создания большого разнообразия паттернов. Это составляет сложность для нас, математиков, так как от нас требуется поддерживать всё это разнообразие паттернов. Поэтому мы задумались, как оптимизировать этот процесс, и преуспели.
Как у нас это получилось? Математически паттерны — это симметрии или, как говорят математики, группы симметрий. Исходя из теории, в нашем случае есть две важные элементарные симметрии — вращательная и трансляционная, — через композицию которых можно создать большое количество разных симметрий, которые в основном и применяются в инженерном моделировании.
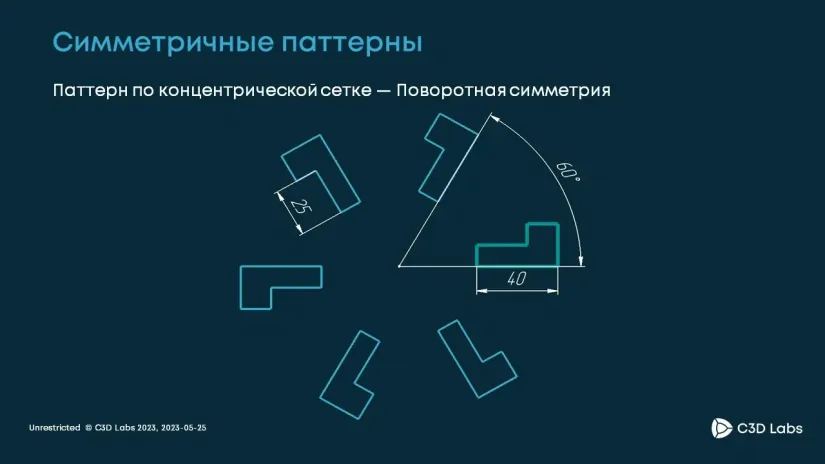
Соответственно, в решателе мы добавили два новых паттерна. Первый паттерн — это паттерн вращения.
Создается он просто. Задается центр вращения, образец и какой-то угловой шаг. Пропорционально этому шагу будут располагаться копии относительно образца. То есть угол, на который копия отклоняется от образца, должен быть кратным шагу.
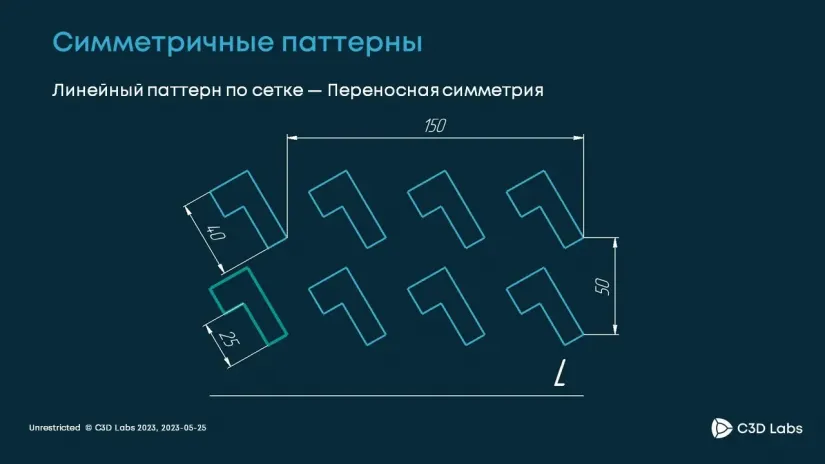
Аналогичным образом мы создали второй вид паттернов — линейные паттерны.
В этом случае перемещение от образца происходит вдоль некоторой прямой на расстояние, кратное заданному шагу. Шаг при этом может быть как варьируемым, так и фиксированным — в зависимости от того, что требуется. Эти паттерны позволяют создавать практически все множество паттернов, необходимых инженерам.
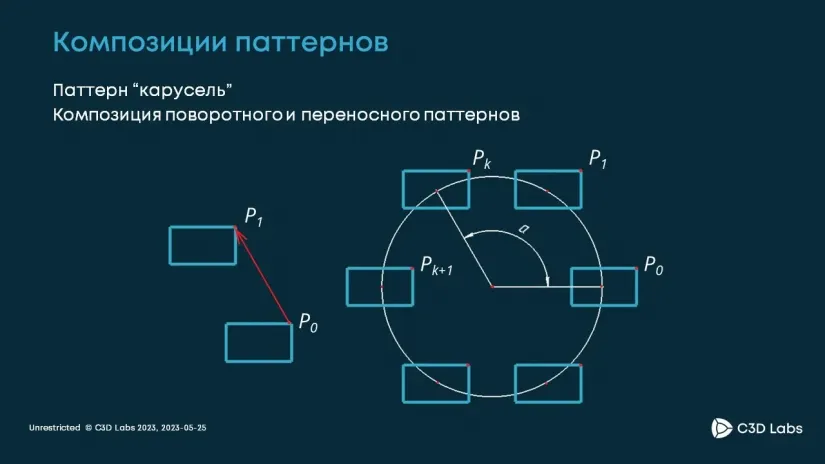
На иллюстрации приведен пример такого составного паттерна — паттерн «карусель», где есть и вращения, и сдвиг вдоль прямой.
В API мы предусмотрели два способа работы с паттернами. Первый способ представлен на этом слайде на примере создания линейного паттерна. Здесь создаётся отрезок, потом определяется линейный паттерн с помощью функции GCE_AddLinearPattern, и после этого рождаются новые геометрические объекты-копии по заданному образцу уже принадлежащими линейному паттерну.
Второй способ проиллюстрирован на примере создания углового паттерна. Когда у вас есть готовые геометрические объекты, их можно связать с паттерном ограничением GCE_AddPatterned.
Следующей новинкой двумерного решателя является управление длиной сплайна.
Теперь можно использовать длину сплайна как управляющий, информационный и интервальный размеры, то есть задавать некоторые границы, в которых длина сплайна может изменяться. Также можно приравнивать длины сплайнов друг к другу и накладывать на сплайн ограничение «точка по метрическому проценту».
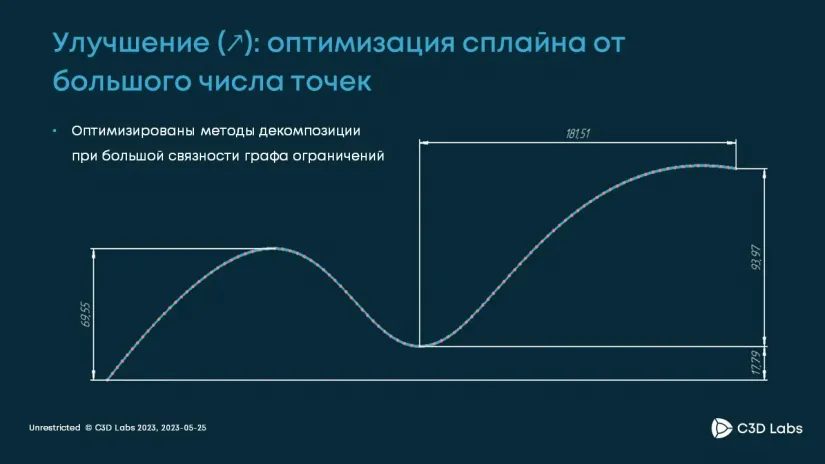
Кроме того, мы значительно улучшили производительность сплайнов.
К нам поступила серия запросов от заказчиков, в которых описывалась похожая ситуация: если в эскизе присутствует множество сплайнов с большим количеством контрольных точек — от 100 и больше, и эти сплайны связаны небольшим количеством ограничений, то в результате получается малосвязный граф, при работе с которым проседала производительность. Отвечая на требования пользователей, мы почти на два порядка повысили производительность в таких сценариях.
Стоит добавить, что для сплайнов был добавлен новый случай касаний — касание с эллипсом.
Еще одна новинка стала следствием двух доработок. Появилась возможность ограничивать положение точки внутри некоторого параметрического участка кривой. Это стало возможным благодаря тому, что теперь в ограничении «точка по проценту на кривой» процент можно задавать как переменную. А также за счет появления нового ограничения GCE_AddBound, которое позволяет ограничить область допустимых значений переменной некоторым интервалом.
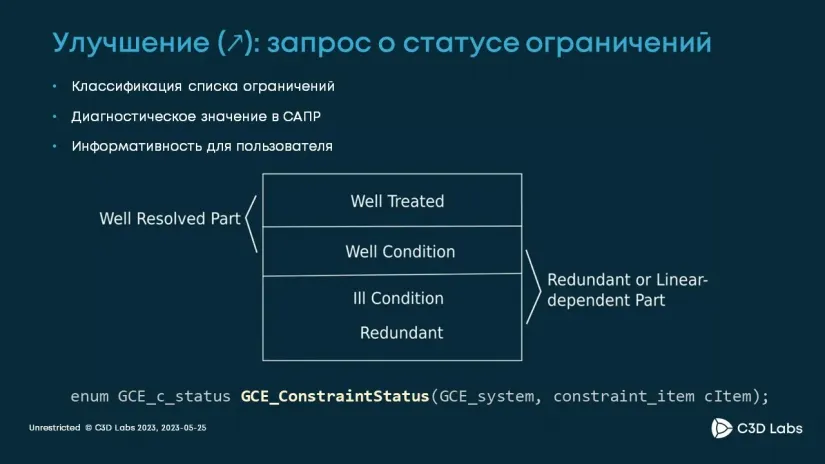
Мы много работаем над анализом степеней свободы. Любому ограничению в решателе присваивается один из четырех статусов, приведенных в таблице.
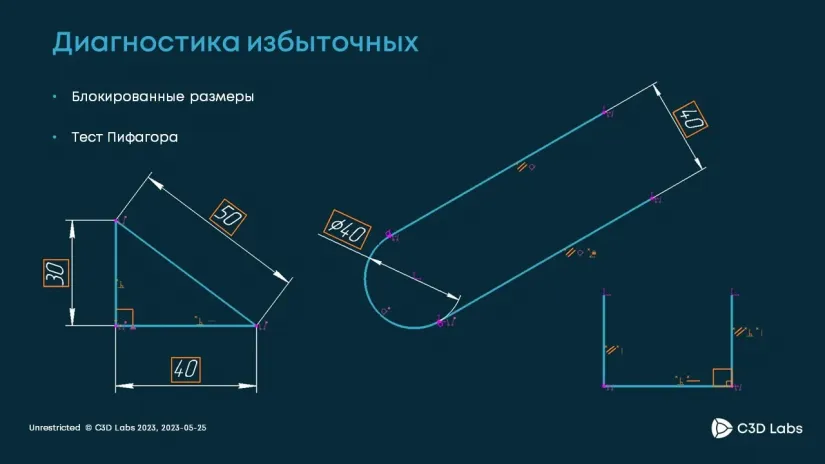
Эти статусы дают возможность разработчикам САПР показать инженерам, что в эскизе что-то идет не так. В этом году мы научились правильно диагностировать большой набор ситуаций, когда инженер формально создал удовлетворенную систему ограничений, но в ней имеются противоречия. Например, вы можете видеть прямоугольный треугольник, в котором инженер задал в качестве управляющих размеров оба катета и гипотенузу.
В итоге он не может изменить ни катет, ни гипотенузу. Ранее мы не могли корректно показать, что это избыточные ограничения. Теперь в целом классе ситуаций мы можем это продемонстрировать. Кроме того, мы повысили локализованность показа избыточности, чтобы инженер увидел непосредственно проблемное место.
Небольшие доработки коснулись размерных ограничений.
Была решена проблема для линейного размера между двумя окружностями, когда они переходили от положительного к отрицательному значению или наоборот. Помимо этого, устранена проблема с вырожденностью биссектрисы, например если угол её раствора равен 180°. Появились две новые функции — ReleaseGeom и ReleaseVariable. Они позволяют разработчику САПР указать решателю, что геометрический объект или переменная ему больше не нужны, и далее не заботиться о порядке их удаления и их времени жизни.
Далее рассмотрим новинки трехмерного решателя, реализация которых потребовала большого труда.
Первая новинка связана с угловыми размерами. Ранее, если пользователь создавал в трехмерном решателе угловой размер, не указывая ось вращения, область значений такого размера находилась в диапазоне от 0° до 180°. Это корректно математически, но неудобно для инженеров, так как углы, допустим в 160° или 200°, либо 90° и 270°, были не отличимы. Мы почти полностью переписали формулировки трехмерных углов, и теперь все трехмерные углы меняются в диапазоне от 0° до 360°. После чего мы добавили новый вид угловых размеров — «интервальные размеры». Так что теперь трёхмерный решатель поддерживает не только управляющие угловые размеры, но и интервальные. Таким образом, все размеры в решателе, как линейные, так и угловые, могут быть интервальными.
Вторая проблема, с которой мы справились, касалась конструирования сборок трехмерных тел. В ходе этого процесса бывает очень важно знать, что геометрический объект фиксирован, то есть полностью определен. В прошлом функция IsWellDefined достаточно часто давала неправильный результат. Мы провели работу в этом направлении, и теперь практически в 100 % случаев функция дает корректные результаты о фиксированности элемента сборки.
Решатель — это сложный продукт, и часто нас спрашивают о том, как внедрить его в свое приложение. Для того чтобы упростить нашим заказчикам работу, мы подготовили пример внедрения трехмерного решателя в приложение с помощью библиотек C3D Vision и Qt. Этот пример доступен теперь в библиотеке примеров C3D Vision. Код примера открытый и может быть использован вами на свое усмотрение.
Нашими стратегическими планами на будущее являются: развитие продвинутого анализа степеней свободы в трехмерном решателе, поддержка сплайнов в трехмерном решателе и автоограничений в двумерном решателе, а также дальнейшее развитие примеров внедрения решателя в пользовательские приложения.
О наших ближайших планах вы можете узнать из нашей дорожной карты, которая доступна на официальном сайте C3D, где вы всегда можете изучить актуальную информацию о наших флагманских продуктах и ходе работ.

Александр Алахвердянц
Ведущий математик-программист
C3D Labs