Одной из основных задач полигонального моделирования является преобразование полигональных моделей в граничное представление. В полигональном ядре C3D PolyShaper уже была возможность вписать в набор полигонов аналитические поверхности: плоскость, цилиндр, сферу, конус или тор. А недавно мы добавили распознавание поверхностей вращения и выдавливания. Расскажем о том, как нам удалось этого достичь.
Рис. 1. Вписывание поверхности выдавливания
Задача сформулирована следующим образом. Имеется некоторая сетка полигонов; требуется получить такую поверхность, которая описывает заданную сетку лучшим образом. Кинематическая поверхность представляется парой объектов: осью вращения или направлением выдавливания и плоской кривой — образующей. Для поверхности вращения образующая строится в полуплоскости, проходящей через ось с одной стороны от неё. Для поверхности выдавливания — в плоскости, которая перпендикулярна направлению. Далее такую плоскость будем называть рабочей.
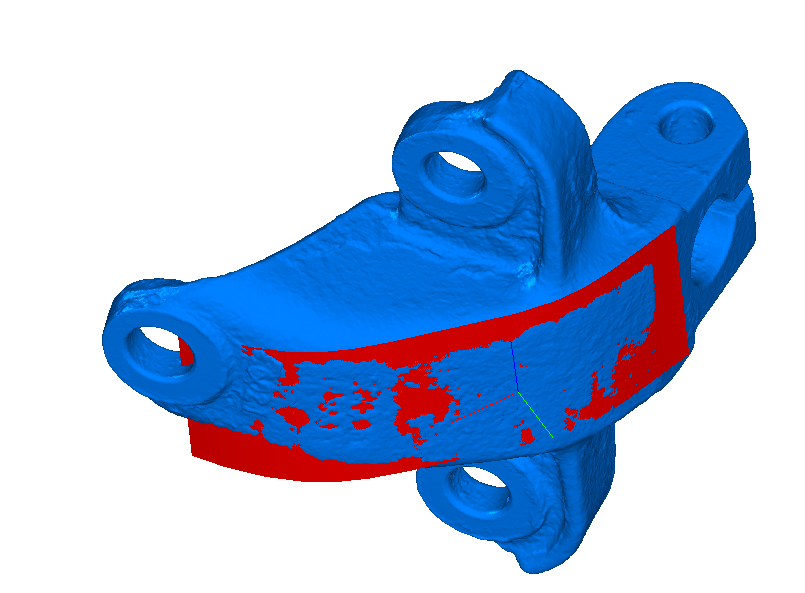
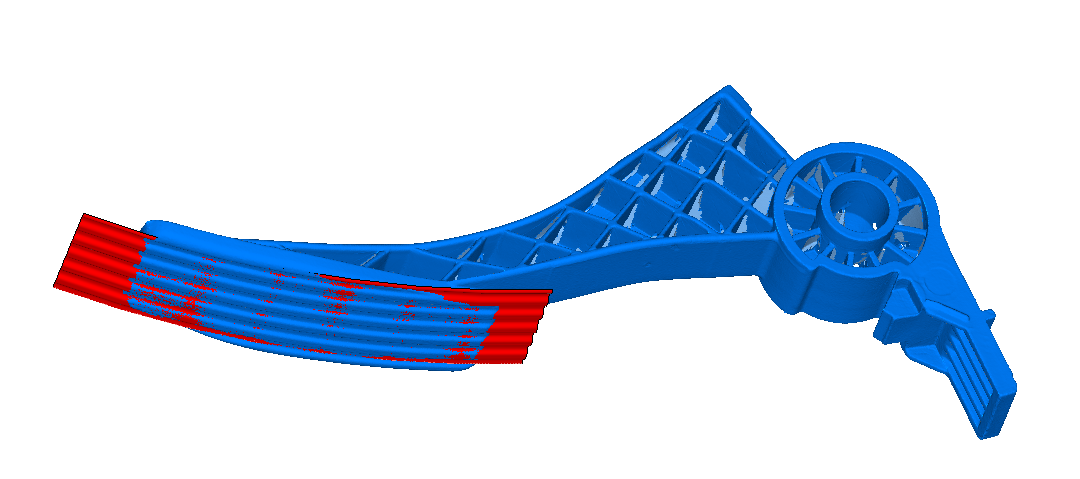
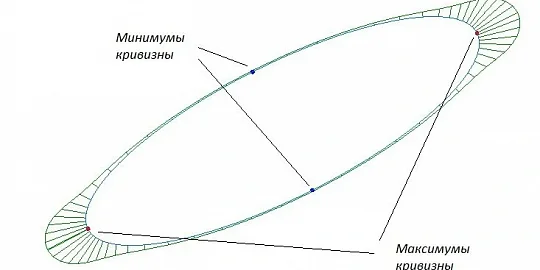
На первом этапе рассчитываем параметры кинематических поверхностей: ось вращения или направление выдавливания. Их можно получить с помощью анализа кривизны или кинематических свойств полигонального объекта. Для сравнения осей, полученных разными способами, мы ввели критерий ошибки — суммарная площадь всех полигонов, спроецированных на рабочую плоскость. Выбираем такую ось, для которой ошибка меньше.
Когда нам уже известны параметры кинематической поверхности, мы можем спроецировать точки исходного полигонального объекта на рабочую плоскость и сформировать на их базе минимальное остовное дерево (spanning tree — дерево, которое проходит через все вершины графа). Для этого сначала составляется плотный граф, в котором каждая вершина соединяется ребром с определённым числом ближайших вершин. Если взять слишком большое число, то последующая сортировка рёбер потребует много времени и вычислительных ресурсов. Если же взять слишком малое число, то граф с большей вероятностью будет несвязным. Меньшее из двух зол здесь — это отсутствие связности, поэтому сначала мы берём небольшое число ближайших соседей, а для соединения отдельных связных компонент применяем итеративную процедуру построения остовного дерева с увеличением числа ближайших соседей. Чтобы ограничить время работы алгоритма, вводится порог максимального количества вершин в графе: если в исходной сетке точек больше, то граф создается по репрезентативной выборке.
Для построения образующей определяем путь между наиболее удалёнными вершинами остовного дерева. Если этот путь проходит через все вершины графа, то итоговый сплайн строится через все точки пути. А если дерево содержит ответвления, то образующей служит аппроксимация найденного пути в дереве с учётом всех его точек. На иллюстрации приведён фрагмент остовного дерева (рёбра подсвечены красным) и образующей (подсвечена синим).
Рис. 2. Остовное дерево и образующая
В коде за вписывание поверхностей отвечает функция FitSurfaceToGrid(). При задании в параметрах MbSurfaceFitToGridParameters типа st_RevolutionSurface или st_ExtrusionSurface будет вписана поверхность вращения или выдавливания соответственно. Также в параметрах можно задать желаемую точность _tolerance.
Пример функции API C3D PolyShaper по вписыванию поверхности вращения:
const MbGrid * pGrid( nullptr ); // … const double tolerance = 0.001; const MbSurfaceFitToGridParameters params( st_RevolutionSurface, tolerance, {} ); MbSurfaceFitToGridResults results; FitSurfaceToGrid( *pGrid, params, results );
Рис. 3. Вписывание поверхности вращения
Распознавание поверхностей выдавливания и вращения является продолжением развития функциональности C3D PolyShaper для реверс-инжиниринга. Новые команды позволят разработчикам ещё лучше преобразовывать сканированные модели в граничное представление.
Павел Стариков
Математик-программист по полигональному моделированию
C3D Labs
